Back to my homepage
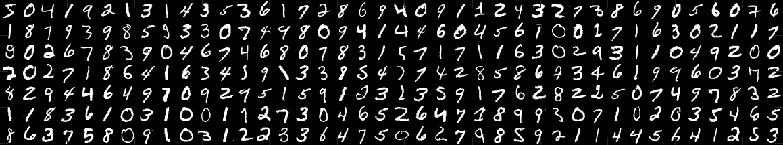
Visitor count (since May 12, 2016):
Fast Counters
MATH 285: Classification with Handwritten Digits
Instructor: Guangliang Chen Spring 2016, San Jose State University
Course description [syllabus] [preview]
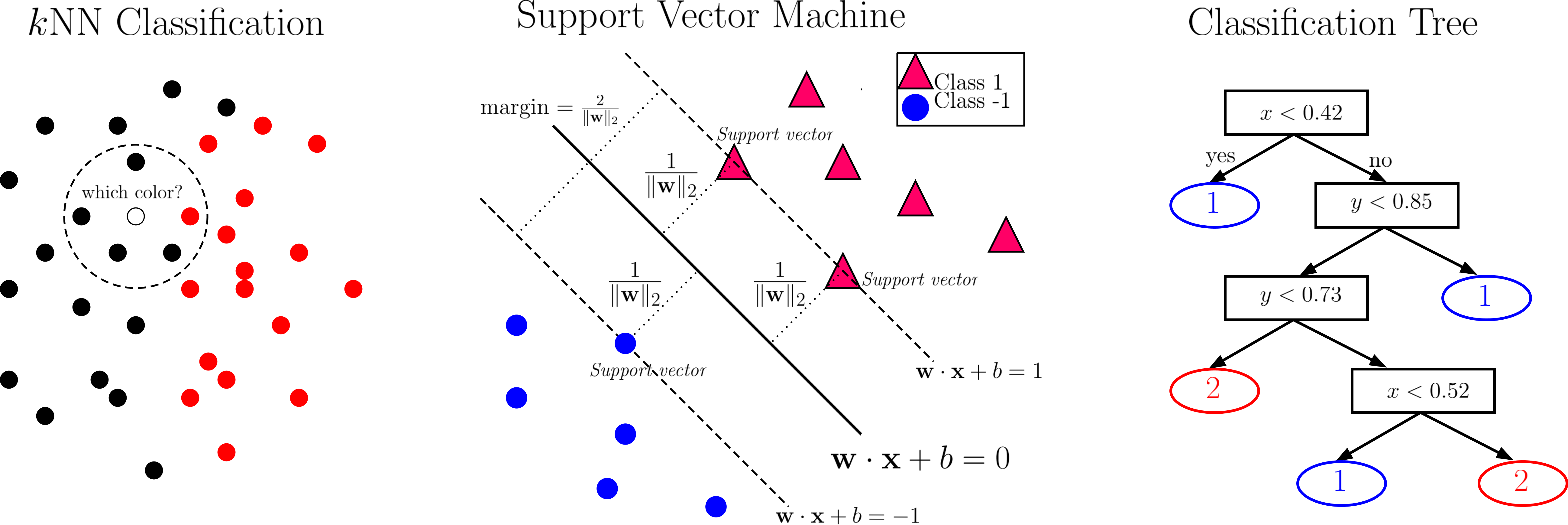 This is an advanced topics course in the machine learning field of classification, with the goals of introducing
This is an advanced topics course in the machine learning field of classification, with the goals of introducing
- Dimensionality Reduction
- Instance-based Methods
- Discriminant Analysis
- Logistic Regression
- Support Vector Machine
- Kernel Methods
- Ensemble Methods
- Neural Networks
all based on the benchmark dataset of MNIST Handwritten Digits.
The course was motivated by a Kaggle competition - Digit Recognizer - and the Fall 2015 CAMCOS at SJSU, and thus has a data science competition flavor. Students will be asked to thoroughly test and compare the different kinds of classifiers on the MNIST dataset and strive to obtain the best possible results for those methods. The use of the MNIST handwritten digits for teaching classification was partly inspired by Michael Nielsen's free online book - Neural Networks and Deep Learning, which notes explicitly that this dataset hits a ``sweet spot'' - it is challenging, but ``not so difficult as to require an extremely complicated solution, or tremendous computational power''. In addition, the digit recognition problem is very easy to understand, yet practically important. To understand more about the rational behind this course, please refer to a reflective linkedin post by the instructor.Course progress
Midterm projects (topic summary)
- Instanced-based classifiers (by Yu Jung Yeh and Yi Xiao)
- Discriminant analysis classifiers (by Shiou-Shiou Deng and Guangjie He)
- Two dimensional LDA (by Xixi Lu and Terry Situ)
- Logistic regression (by Huong Huynh and Maria Nazari)
- Support vector machine (by Ryan Shiroma and Andrew Zastovnik)
- Ensemble methods (by Mansi Modi and Weiqian Hou)
- Neural networks (by Yijun Zhou)
Final projects [instructions]
Some ideas include kernel knn, kernel discriminant analysis, application to USPS handwritten digits, tuning the penalty parameter C in SVM, and deskewing of MNIST digits. Talk to me if you need more ideas or have specific questions.More learning resources
Handling singularity in LDA/QDA
- Psuedoinverse LDA
- Regularized LDA (see Section 4.3.1, page 112 of recommended textbook)
- PCA + LDA
- Direct LDA
- QR + LDA;
- 2DLDA+ LDA;
Programming languages
- MATLAB:
- Common Matlab commands;
- Online tutorials (see here for a simple one);
- Statistics and Machine Learning Toolbox Documentation;
- Python:
- R:
Useful course websites
- Prof. Veksler's CS9840a Learning and Computer Vision at University of Western Ontario
- Andrew Ng's CS 229 Machine Learning at Standford University
- Manik's CSL 864 - Special Topics in AI: Classification at Microsoft
Data sets
- USPS Zip Code Data
- UCI Machine Learning Repository
- LibSVM data sets
- Extended Yale Face Database B
- Oxford Flowers Category Datasets
Instructor feedback
This is an experimental course in data science, being taught at SJSU for the first time. Your feedback (as early as possible) is encouraged and greatly appreciated, and will be seriously considered by the instructor for improving the course experience for both you and your classmates. Please submit your annonymous feedback through this page.Visitor count (since May 12, 2016):
Fast Counters